Grid Mapping:
The recursive backtracker algorithm we discussed in the previous article can be easily improvised and implemented for grid mapping. This can be understood by understanding that the algorithm is essentially a search algorithm designed to locate the destination point anywhere on a grid with obstacles and thus it will check every point on the grid. So if the bot is given only the starting point, it will go to all points on the grid and return back to the start and when that happens we can program it to stop. Now we know if we have stored all the points that the bot has visited, these will indicate open positions on the grid and the remaining points will become the points containing obstacles (in this case platforms that provide the path for the upper bot).
Shortest Path Algorithm: There are quite a few algorithms that can be used to find the shortest paths in a maze or a grid. The common thing among them all is that a map of the grid is required beforehand. One such popular algorithm is the Dijkstra’s Algorithm. The algorithm basically finds the shortest number of steps between each node of the grid and the starting point.
Pseudo-Code (in C#):
The following function runs several passes through the given map and stores the shortest distance of each node from the starting point.
void Pathfind(starting point)
{
int heroX = startingPoint.X;
int heroY = startingPoint.Y;
if (heroX == -1 || heroY == -1)
{
return;
}
// Hero starts at distance of 0.
_squares[heroX, heroY].DistanceSteps = 0;
while (true)
{
bool madeProgress = false;
// Look at each node on the grid. This loop is executed more than once
foreach (Point mainPoint in Squares())
{
int x = mainPoint.X;
int y = mainPoint.Y;
// If the square is open, look through valid moves given
// the coordinates of that square.
if (SquareOpen(x, y))
{
int passHere = _squares[x, y].DistanceSteps; //Number of steps from the starting point to this point
foreach (Point movePoint in ValidMoves(x, y))
{
//All points that can be moved to from the current point are checked
int newX = movePoint.X;
int newY = movePoint.Y;
int newPass = passHere + 1; //Surrounding points are one more than the distance of the current point from the starting point
if (_squares[newX, newY].DistanceSteps > newPass)
{
//Change the distance steps value only if the new distance is less than distance already stored
_squares[newX, newY].DistanceSteps = newPass;
madeProgress = true;
}
}
}
}
if (!madeProgress)
{
break;
}
}
}
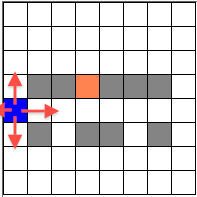
Let us assume that the code is at a point (0, 4) using this function. Now it is required to check all the four directions. This point is at 3 steps away from the starting point so now (0, 3) (1, 4) and (0, 5) will be 4 steps away from the starting point. This will be stored in the corresponding distance steps variables of the points Note that the ending point is not required anywhere in this function as the code finds the least number of steps required to reach any node on the grid from the designated starting point. The above function continuously scans the grid until all squares have been marked with the lowest distances from the starting point. When that happens madeProgress variable remains false and the program exits from the loop.
**Runs of the Pathfinder loop through the map look something like this : **
[caption id=”attachment_674” align=”alignleft” width=”203” caption=”First pass through the map”]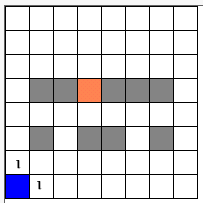
[/caption]
[caption id=”attachment_672” align=”alignleft” width=”203” caption=”Second Pass”]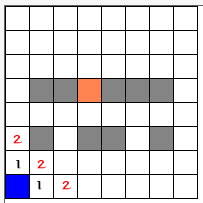
[/caption]
[caption id=”attachment_673” align=”alignleft” width=”203” caption=”Third Pass”]
[/caption]
Marking the path from start to finish requires another function :
private void HighlightPath(ending point)
{
int pointX = endingPoint.X;
int pointY = endingPoint.Y;
if (pointX == -1 && pointY == -1)
{
return;
}
while (true)
{
// Look through each direction and find the square
// with the lowest number of steps marked.
Point lowestPoint;
int lowest = 100; //A default value to compare distances with
foreach (Point movePoint in ValidMoves(pointX, pointY))
{
//Find the surrounding square with least value of distance steps
int count = _squares[movePoint.X, movePoint.Y].DistanceSteps;
if (count < lowest)
{
lowest = count;
lowestPoint.X = movePoint.X;
lowestPoint.Y = movePoint.Y;
}
}
if (lowest != 100)
{
// Mark the square as part of the path if it is the lowest
// number. Set the current position as the square with
// that number of steps.
_squares[lowestPoint.X, lowestPoint.Y].IsPath = true;
pointX = lowestPoint.X;
pointY = lowestPoint.Y;
}
else
{
break;
}
if (_squares[pointX, pointY].ContentCode == SquareContent.Hero)
{
// We went from monster to hero, so we're finished.
break;
}
}
}
Now this function marks the shortest path, starting from the ending point, it locates those surrounding nodes which require the least number of steps to reach from the starting point. The loop ends when the code reaches the square which contains the starting point.
**Resources: **This tutorial has been compiled using the following resources: http://www.dotnetperls.com/pathfinding
In the link you can find a software written in C# that demonstrates the algorithm as well. You can also go through articles and videos on the Internet regarding Dijkstra’s Algorithm.